8/27 数学・別解４

__

前回に引き続き、４つ目の別解をご紹介申しあげる。 【問題】 上の図において、二等辺三角形ＡＢＣで、 底角∠Ｂ,∠Ｃの二等分線が辺ＡＣ,ＡＢと交わる点をそれぞれＤ,Ｅとする。 このとき、 ＥＢ＝ＤＣ であることを証明しなさい。 ［別解４］ BC＝a, AB＝AC＝b とする。 CEは∠ACBの二等分線なので、 三角形における角の二等分線と線分の比との関係から BC：AC＝EB：AE すなわち a：b＝EB：AE・・・・① また　AE＝AB－EB＝b－EB・・・② ①,②より a：b＝EB：b－EB・・・・・・・③ よって a(b－EB)＝bEB 展開して ab－aEB＝bEB EBについてまとめると ab＝(a＋b)EB a+b≠0であるから EB＝ab／(a＋b)・・④ BDは∠ABCの二等分線なので、前記と同様に BC：AB＝DC：AD すなわち a：b＝DC：AD・・・・⑤ また　AD＝AC－DC＝b－DC・・・⑥ ⑤,⑥より a：b＝DC：b－DC 前記の③から④までと同様な変形をおこなうと DC＝ab／(a＋b) ・・・・・・・⑦ ④,⑦により EB＝DC この別解は、前回申しあげたように、現行教科書の内容を超える。 しかし、ご紹介したすべての解答の中で最も美しい解答だと小生は思うのでありますが、貴下は如何？ なに？　すべて美しくないって？ 退場を命じます！ 中学生,高校生の数学の勉強,学習,受験 勉強も教える数学受験学習塾

__

8/20 数学・前回の別解３つ

__

【問題】 上の図において、二等辺三角形ＡＢＣで、底角∠Ｂ,∠Ｃの二等分線が辺ＡＣ,ＡＢと交わる点をそれぞれＤ,Ｅとする。 このとき、ＥＢ＝ＤＣ であることを証明しなさい。 [別解１] ＢＤとＣＥとの交点をＦとする。 （あらすじ：△ＥＢＦと△ＤＣＦが合同であることを言って、「ゆえにＥＢ＝ＤＣ」 とキメル。 合同をいうために、△ＦＢＣが二等辺三角形になることからＦＢ＝ＦＣを使うのがポイントでしょうか。） △ＥＢＦと△ＤＣＦで、 △ＡＢＣは ＡＢ＝ＡＣの二等辺三角形だから ∠ＡＢＣ＝∠ＡＣＢ・・・・① 仮定から ∠ＥＢＦ＝∠ＡＢＣ／２・・② ∠ＤＣＦ＝∠ＡＣＢ／２・・③ ①,②,③ より ∠ＥＢＦ＝∠ＤＣＦ・・・・④ ところで、△ＦＢＣにおいて、 仮定より ∠ＦＢＣ＝∠ＥＢＦ・・・・⑤ ∠ＦＣＢ＝∠ＤＣＦ・・・・⑥ ④,⑤,⑥ より、 ∠ＦＢＣ＝∠ＦＣＢ ２つの角が等しい三角形はそれらの角を底角とする二等辺三角形であるから、 △ＦＢＣは、∠ＦＢＣと∠ＦＣＢとを底角とする二等辺三角形である。 よって ＦＢ＝ＦＣ・・・・・・・・⑦ さらに、対頂角であるから ∠ＥＦＢ＝∠ＤＦＣ・・・・⑧ ④,⑦,⑧により １辺とその両端の角がそれぞれ等しいので （１辺：⑦、その両端の角：④,⑧） △ＥＢＦ≡△ＤＣＦ ゆえに ＥＢ＝ＤＣ （かなりシンドイ。夏むきじゃない！） [別解２] （あらすじ：まず、△ＡＣＥと△ＡＢＤが合同であることをいって、ＡＥ＝ＡＤをみちびく。 つぎに、これとＡＢ＝ＡＣとから引き算の式でＥＢとＤＣを書けば結論がいえる。） △ＡＣＥと△ＡＢＤで、 仮定から ＡＣ＝ＡＢ・・・・・・・・① 共通な角だから ∠ＥＡＣ＝∠ＤＡＢ・・・・② また、仮定から ∠ＡＣＥ＝∠ＡＣＢ／２・・③ ∠ＡＢＤ＝∠ＡＢＣ／２・・④ △ＡＢＣは ＡＢ＝ＡＣの二等辺三角形だから ∠ＡＣＢ＝∠ＡＢＣ・・・・⑤ ③,④,⑤より ∠ＡＣＥ＝∠ＡＢＤ・・・・⑥ ①,②,⑥により １辺とその両端の角がそれぞれ等しいので △ＡＣＥ≡△ＡＢＤ したがって ＡＥ＝ＡＤ・・・・・・・・⑦ ところで、 ＥＢ＝ＡＢ－ＡＥ・・・・・⑧ ＤＣ＝ＡＣ－ＡＤ・・・・・⑨ よって①,⑦,⑧,⑨より ＥＢ＝ＤＣ [別解３] （あらすじ：ここまでの３つの解答は三角形の合同を利用したが、ここでは円を利用する。　まず、４点Ｄ,Ｅ,Ｂ,Ｃが同一円周上にあることを言い、つぎに、弧ＥＢ,弧ＤＣに対する円周角が等しいことを言って結論をみちびく。） △ＡＢＣは ＡＢ＝ＡＣの二等辺三角形だから ∠ＡＢＣ＝∠ＡＣＢ・・・・① 仮定から ∠ＥＢＤ＝∠ＡＢＣ／２・・② ∠ＤＣＥ＝∠ＡＣＢ／２・・③ ①,②,③ より ∠ＥＢＤ＝∠ＤＣＥ・・・・④ また、３点Ｄ,Ｅ,Ｂを通る円において、点Ｃは弦ＥＤについて弧ＥＢＤと同じ側にある。 このことと④とにより、点Ｃは弧ＥＢＤ上にある。 すなわち、４点Ｄ,Ｅ,Ｂ,Ｃは同一円周上にある。・・＠ ところで、 仮定から ∠ＢＣＥ＝∠ＤＣＥ・・・・⑤ ∠ＣＢＤ＝∠ＥＢＤ・・・・⑥ ④,⑤,⑥より ∠ＢＣＥ＝∠ＣＢＤ・・・・⑦ １つの円において、等しい円周角に対する弧は等しいから ＠,⑦より 弧ＥＢ＝弧ＤＣ １つの円において、等しい弧に対する弦は等しいので ＥＢ＝ＤＣ うっかりしていて申しわけないが、この[別解３]は現行教科書－平成１３年検定－の内容を超える。 したがって、新課程で学ばれた方は、この解答が思い浮かばなくて当然である。 アシカラズ・・・。 なお、前回、もうひとつ非一般的な解答がある　と申しあげたが、それは次回にご紹介させていただくことにする。 あらすじは、三角形における角の二等分線と線分の比との関係を利用するものであって、小生の好みでは５つの解答のうちでもっともビューティフルな解答になると思われるが、これこそ現行教科書を超える。 中学生,高校生の数学の勉強,学習,受験 勉強も教える数学受験学習塾

__

8/13 数学・結論は使えない

__

今回は「証明問題」について、ひじょうに基本的なことであるにもかかわらず、よくお間違えになることをご紹介させていただく。 まず、つぎの問題と誤答をご覧いただきたい。 問題は、中２数学の教科書（Ｋ社）に載っているものである。 【問題】 上の図において、二等辺三角形ＡＢＣで、底角∠Ｂ,∠Ｃの二等分線が辺ＡＣ,ＡＢと交わる点をそれぞれＤ,Ｅとする。 このとき、 ＥＢ＝ＤＣ であることを証明しなさい。 （蛇足だが、「証明」とは、「あることがらが正しいことを、すでに正しいと認められたことがらを根拠にして、すじ道をたてて説明すること」である。） [誤答］ △ＥＢＣと△ＤＣＢで、 △ＡＢＣは ＡＢ＝ＡＣの二等辺三角形だから ∠ＥＢＣ＝∠ＤＣＢ・・・① また、 ＢＣ＝ＣＢ・・・・・・・② ＥＢ＝ＤＣ・・・・・・・③ ①,②,③より、 ２辺とその間の角がそれぞれ等しいので △ＥＢＣ≡△ＤＣＢ したがって ＥＢ＝ＤＣ 上記の証明のどこがマチガイだろうか？ 賢明なる読者様のお気付きのとおり、証明の過程において、これから証明すべきことがらである ＥＢ＝ＤＣ を使っている（ ③ ）ことである。 「証明すべきことがら」とは、すなわち「結論」である。 「Ａさんを殺した犯人はＢだ」という結論にいたる理由を説明するのに、 "「ＡさんはＢに恨まれていた」そして「Ａさんを殺した犯人はＢ」なのであるから「Ａさんを殺した犯人はＢだ」" というナンセンスなことは、シャーロック・ホームズは決して言わないであろう。 くどいようだが、「証明の過程では、結論は使えない」のである。 しかし、この「証明の過程で結論を使ってしまうマチガイ」はかなり多い。 このマチガイを防ぐために、問題の結論の部分（この問題では ＥＢ＝ＤＣ）を四角い枠（ハート形でもよい）で囲んでいただくことをオススメ申しあげる。 はなしのついでに、解答（正答）を下記させていただく。 [解答] △ＥＢＣと△ＤＣＢで、 △ＡＢＣは ＡＢ＝ＡＣの二等辺三角形だから ∠ＥＢＣ＝∠ＤＣＢ・・・① また、 ＢＣ＝ＣＢ・・・・・・・② 仮定から ∠ＥＣＢ＝∠ＡＣＢ／２＝∠ＤＣＢ／２・・③ ∠ＤＢＣ＝∠ＡＢＣ／２＝∠ＥＢＣ／２・・④ ①,③,④ より ∠ＥＣＢ＝∠ＤＢＣ・・・⑤ ①,②,⑤ より、 １辺とその両端の角がそれぞれ等しいので △ＥＢＣ≡△ＤＣＢ したがって ＥＢ＝ＤＣ でゴザル。 ところで、解答はこのほかに３通り（非一般的なものも含めると４通り）ある。 ひとつ（ではなくて３つ）考えてみていただきたいが、如何？ ３通りの解答は、次週（'05/8/15～21）の弊ブログに掲載させていただく予定である。 （ヒントをご希望でしたら、その旨お申し出ください。希望者様のブログ宛、またはノンブロガー様には弊ブログのコメント欄にて、ヒントを提供させていただきます。） 中学生,高校生の数学の勉強,学習,受験 勉強も教える数学受験学習塾

__

8/6 数学・「１では？」 と考える

％とか歩合などの割合の問題もわりあいわかりにくい（グャギじやお）もののひとつである。 まずは、かんたんな問題をやってみよう。 【問題Ａ】 12,340円の５％はいくらか？ [解説] 5％とは、もとの量（12,340円）の 5/100（または 0.05）だから、 12,340 × 5/100 = 12,340 × 1/20 = 617 (円)　・・・（答） とおやりになるのは、もちろん大正解なのだが、「 5/100 を掛ける」というアイデアが出てこない場合は、タイトルにあるように、「１では？」すなわち「１％では？」と考えるとよい。 ％とは、もとのもの全体を 100％ としているから、１％とは、もとのものを 100個に切りきざんだ切れ端のうちの１個なので、もとのものを 100で割ればでてくる。 すなわち 12,340円の１％は 12,340 ÷ 100 (円) 100で割ることは 1/100 をかけることと同じだから、12,340円の１％は 12,340 × 1/100 (円)となる。 そして、5％は１％の５倍だから、これ（12,340 × 1/100）の５倍、つまり５をかければよく、 12,340 × 1/100 × 5　となり、 5 は 5/1 のことだから、 1/100 × 5 = 1/100 × 5/1 = 1×5/100×1 = 5/100 したがって４行上の式（12,340 × 1/100 × 5）は 12,340 × 5/100 となって[解説]のはじめの方にでてきた式に一致する。 これは、パーセントの定義である「ある量の 1/100 を１％という。」（本来の定義文とは異なるかもしれないが意味的には同じなのでご容赦を）にもどって考えているのでもあって、わからなくなったら、あるいは教える側として、このように定義にもどるのもなかなか有効な手段である。 （定義：「概念の内容を限定すること」　ひらたく言えば「ことばの意味を決めている文」ということでしょうか。） では、つぎの問題をお考えいただきたい。 【問題Ｂ】 12,340円の a％はいくらか？ 【問題Ｃ】 Ｍ円の a％はいくらか？ 解答は、コメントをご覧ください。 中学生,高校生の数学の勉強,学習,受験 勉強も教える数学受験学習塾

7/30 数学・よくある間違い

今回のお勉強は、間違えやすい分数の計算について。 【 問題 】 つぎの式の右辺に間違いが１つある。それは何か？（左辺は正しいとする） 4a-5 _ 7a+8 ＿ 8a-10-7a+8 ..3......6..￣......6 【 解答 】 分子の最後尾8の符号＋。 一応理由を説明すると、 _ 7a+8 ＿ _ 1×(7a+8) ....6..￣...6 ＿ _ 7a _ 8 ￣....6...6 ＿ -7a-8 ￣....6 であるので、+8 は間違いで、－8 が正解。 この間違いはひじょうに多いので、ご用心ご用心。 数学の勉強,学習,受験 勉強も教える数学受験学習塾

7/22 数学・正直者はバカをみる？

「正直者はバカをみる」とはよく聞くコトバ（しかし教育者が口にすべきでないコトバ）だが、数学の計算でもあてはまる。 例によって実例をあげてご説明させていただく。 【問題】つぎの計算をせよ。 63×75 25×18 【解答例 Ａ】 63×75＝4725　25×18＝450　だから 4725 450 約分して 21 2 と問題に正直？に掛け算を先におこなう方法。 【解答例 Ｂ】 63と18を9で約分して　63→7　18→2 75と25を25で約分して　75→3　25→1　となるので 7×3 ＿ 21 1×2 ￣ 2 と約分をまっ先におこなう方法。 ２つの解答例をくらべれば、【解答例 Ａ】は ①掛け算という余計な手間を食い ②4725 と 450 の約分が数が大きいのでやりにくく ③やることが多いのでミスを犯す率も高くなる。 のであって、バカをみているのは一目瞭然であろう。 平方根の計算（中３の範囲）でも同様であって、根号の中の数を根号の外に出す場合、たとえば根号の中身が 6×42　であれば、 6×42＝252 と掛け算をおこなってから考えるのではなくて、 6×42＝(2×3)×(2×3×7)＝(2×2)×(3×3)×7 として 2 と 3 を根号の外に出す方がお利口さんである。 ( 6×6×7 として 6 を根号の外に出す方がさらにお利口さんなことはモチロンである。) とまぁこのように掛け算はすぐにやらない方がバカをみず、御利益にありつける場合が多いようである。 閑話休題。ふだん習慣的におこなっていること（数学にかぎらない）の中にバカをみていることがないかどうか再点検してみると以外な新発見があったりして、人生のたのしみがふえるんじゃないか、と小生は思いますが、貴殿は如何？ 勉強も教える数学受験学習塾

7/16 数学・「書く」は偉大

今まで３回にわたって「書くことの御利益(ごりやく)」をご紹介した。 今回はこれらをまとめてみよう。 [6/15 間違い暗算] では、 ２つのタスク（たとえば「符号（＋－）を変えること」と「式を展開する（カッコを外す）こと」）を暗算で同時におこなうとミスを誘発するので、タスクを完全に分け、各タスクをそれぞれ紙に書いておこなうべし。 というはなしで、書くことの御利益は 【ミスを減らす】 ということであった。 [6/27 書けば解ける] では、 頭の中だけで考えてわからないときは、紙に書いてみると問題の全体像や解決策が見えてくる。 すなわち書くことの御利益は 【思考力増強】 であるというはなしであった。 [7/6 図形に書き込む] では 図形に、わかっていることを（長さや角が等しい、とか平行とかを記号で）書き込むと問題の解決策を見つけやすい。 ということで、書くことの御利益は上とおなじく 【思考力増強】 であった。 まとめると、書くことの御利益は 【ミスを減らす】と【思考力増強】 の２つということになるが、もうひとつ 【記録（or保存）】 という一面もある。 ところで もし「書く（および描く）」ということが存在していなかったら、現在の文明社会も存在しないであろう。 科学者は紙とエンピツを取り上げられたら、あたらしい理論を展開することができるだろうか？ エジソンだって書くことなしに発明ができただろうか？ 文学作品も絵画も存在しないわけだ。 そう想うと「書く」とは偉大なことだと思う。 これは地球上では人類だけがもつ特権だ。 この特権を利用しない手はない。 「めんどっちい」とか「ノートや教科書がきたなくなる」とかおっしゃらずに、おおいにこの特権を行使していただきたい。 切望申しあげる。 数学の勉強,学習,受験 勉強も教える数学受験学習塾

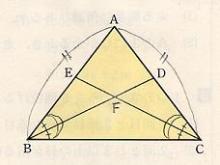
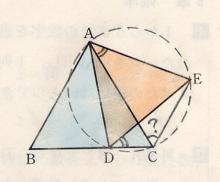
7/7 数学・図形に書き込む

前回（6/27 書けば解ける）の続編でありまして、 「図形に、わかっていることを（長さや角が等しい、とか平行とかを記号で）書き込むと"御利益"がある」 というおはなし。 前回と同様、問題を例にして説明させていただく。 【 問題 】 図のように、頂点Ａが重なる正三角形ＡＢＣと正三角形ＡＤＥがある。 Ｄが辺ＢＣ上にあるとき、∠ＡＣＥの大きさを求めよ。 （中学２年の数学教科書に載っている問題である。） まず、記号が書き込まれていない下図を見て、お考えいただきたい。 なかなか妙案が浮かばないのではないだろうか？ （スラスラ出来ちまった方は前回同様、以下の駄文はお読みになる必要はない。 ゲームのつづきでもやってください。） では、長さについて等しいことを示す記号を書き込んだ次の図をご覧いただきたい。 すると、求めるべき∠ＡＣＥ（？マークの角）を含む△ＡＣＥと、それと形が似ている△ＡＢＤの二つについて、等しいという記号がついている辺は、 ＡＣ＝ＡＢ・・・①　と ＡＥ＝ＡＤ・・・② であることが容易にわかる。 ここで、もし ∠ＣＡＥ＝∠ＢＡＤ・・・③ であれば、①,②といっしょになって、三角形の合同条件のひとつである 「２辺とその間の角がそれぞれ等しい」 がＯＫになるので、両三角形は合同になり、したがって ∠ＡＣＥ＝∠Ｂ＝６０° となって、一件落着と相成る。 （∠Ｂ＝６０°の理由：△ＡＢＣは正三角形なので３つの角はすべて６０°） そこで、③がＯＫかどうかだが、③の両辺は、正三角形の１つの角（∠ＤＡＥ、∠ＢＡＣ）すなわち６０°からそれぞれ同じ∠ＤＡＣを差し引いたものであって、式に書けば、 ∠ＣＡＥ＝∠ＤＡＥ－∠ＤＡＣ＝６０°－∠ＤＡＣ ∠ＢＡＤ＝∠ＢＡＣ－∠ＤＡＣ＝６０°－∠ＤＡＣ よって ∠ＣＡＥ＝∠ＢＡＤ （③と同じ） であるから、③は１００％ＯＫである。 したがって、正解は ∠ＡＣＥ＝６０°　でゴザル。 さて、はなしを本題にもどして、この問題が解けるか否かは、「△ＡＣＥと△ＡＢＤが合同であること」に気がつくことに懸かっており、上の２つの図のどちらが気づき易いかといえば、モチ、下の記号入りの図の方であろう。 「上の図の方」とお答えの方には、お臍がまっすぐかどうかご点検をおすすめする。 以上のことから、図に記号を書き込むと御利益があることをご理解いただけたと思う。 おおいに利用していただきたい。 なお、下記のようなビューティフルな別解もあるので、ご参考まで。 ただし、現行（H13年検定）の教科書の記述を少し超えるが。 （旧教科書ではセーフである。） 【別解】 △ＡＤＥは、はじめ、ＡＤ,ＡＥがそれぞれＡＢ,ＡＣに重なる位置にあったとし、その位置から点Ａを中心として反時計回りの向きに∠ＣＡＥだけ回転移動したと考える。 また、はじめの位置では ＤＥ//ＢＣ すなわち ＤＥとＢＣのなす角は０°であったから ∠ＣＡＥ＝∠ＣＤＥ　（両方とも回転した角） さらに、点Ｄ,Ｃ,Ｅを通る円において、点Ａは弦ＣＥについて弧ＣＤＥと同じ側にある。 この２つのことから、定理（＊）により、点Ａは弧ＣＤＥ上にあることになる。 すなわち４点Ａ,Ｄ,Ｃ,Ｅ は同一円周上にある。 そして、∠ＡＣＥと∠ＡＤＥは共通の弧ＡＥに対する円周角になっている。 したがって定理（＊＊）により ∠ＡＣＥ＝∠ＡＤＥ＝６０° （別解ＥＮＤ） 定理（＊） 円Ｏで、点Ｑが弦ＡＢについて弧ＡＰＢと同じ側にあって、 ∠ＡＱＢ＝∠ＡＰＢならば、点Ｑは弧ＡＰＢ上にある。 （現行教科書では削除されている。） 定理（＊＊） 同じ弧に対する円周角の大きさはすべて等しい。 この別解をビューティフルと思っていただけるか否かは、もちろん貴下のご自由である。 数学の勉強,学習,受験 勉強も教える数学受験学習塾

6/27 数学・書けば解ける

前回（6/15）は、１行書き加えることで計算ミスを大幅に減らせることをご伝授申しあげた。 今回はその続編で、「紙に書く」ということは、ひじょうに強力な思考力増強の助っ人であり、ぜひ貴君のパートナーにしていただきたい、ということである。 なぜ、紙に書くことが思考力増強になるのかというと、その端的な例は、図形の問題である。 貴君はつぎの問題を、紙に書くことなしに３分以内に解けるだろうか？ （Ｋ社の中学２年の数学教科書に載っている問題である） （問題１） 平行四辺形ＡＢＣＤの４つの角 ∠Ａ,∠Ｂ,∠Ｃ,∠Ｄ の二等分線でつくられる四角形はどんな四角形か？ どんな四角形？ と来たら答えは、平行四辺形、正方形、長方形、ひし形、台形 のどれかで、台形はないだろうから、それ以外の４つのどれかで、あてずっぽうでも正解の確率は４分の１なのだが、ここでは、あてずっぽうは禁止させていただく。 この問題を紙に書かずに３分以内に解けたら、小生の駄文をお読みになる必要はない。 ゲームでもやってください。 頭の中だけで考えて答えが出なかった方は、紙に図をお描きください。 定規を使って、できるだけ正確に。　分度器は出さなくて結構。 さて、描き終えたら、平行四辺形ＡＢＣＤの中にできた四角形をシカとご覧いただきたい。 とくに、４つの角にご注目。 なにやら直角のように見えませんかな？ 平行四辺形をほそ長く描いた方は長方形っぽく、平行四辺形をひし形のように描いた方は正方形のように見えると思う。 ピンポーン！正解は「長方形」なのだ。 あとは、その理由、つまり４つの角が９０°になることを考えればいいだけだ。 （ヒントはこの駄文へのコメント参照） いつもこのように超うまくいくとは限らないが、「書（描）くこと」が強力な助っ人になり得ることはお分かりいただけたのではないかと思う。 まぁ、図形の問題で図を描くのは、あたりまえのはなしだが。 しかし、この教科書にはご親切にも図がちゃんと載っているのだ。 本題からそれるが、これはよくないと思う。 「文章を読んで、その意味するところを図に表す」という知的作業をさせないわけだから、生徒さんの知的能力の発達を阻害しているのではないだろうか？ それはさておき、「書くこと」が有効なのは図形だけの専売特許ではない。 つぎの問題を、計算以外は紙に書かずに解いてみていただきたい。 （中学１年の数学教科書に載っている１次方程式の問題である） （問題２） 姉が駅に向かって歩いて家を出てから６分後に、弟が同じ道を自転車で追いかけた。 姉の歩く速さを分速５０m、弟の自転車の速さを分速２００m とすると、弟は家を出てから何分後に姉に追いつくか？ 私立中学受験のための勉強をしているお子さんならば簡単に解いてしまうかもしれないが、そういう特別な勉強をしていない方には紙なしではキツイであろう。 また、ふだんから「書いて考えること」に慣れていない生徒さんは、なにを書けば思考の助けになるのか、わからないのではないか。 では、なにを書けばよいかというと、問題を読んで思いうかぶイメージを図にしてみることだ。 たぶん、姉が歩き、弟が自転車で走る姿がイメージされるだろう。 動画を描くわけにいかないから、ある瞬間の図を描くこになる。 ではどの瞬間がよいか？ １． 問題に「弟は家を出てから何分後に姉に追いつくか？」とあるから、まずは弟が姉に追いついた瞬間が最重要である。 ２． また、「姉が駅に向かって歩いて家を出てから６分後に、弟が同じ道を自転車で追いかけた。」というのが問題を複雑にしているので、これを図にしてわかりやすくしてみたい。 そこで選びたい瞬間は、姉が家を出る瞬間か、弟が家を出る瞬間か、のどちらかになるが、結論を先にいえば、弟が家を出る瞬間がよい。 なぜかというと、６分ぶんの距離だけ弟の先を行く姉の姿を書き込めるからだ。 この２つを、わかりやすいように時間の流れにしたがい、２,１の順番で図にしてみる。 姉を [姉]、弟を ○弟○ とあらわす。 【弟が家を出る瞬間】 ○弟○＿＿＿＿＿＿＿＿[姉] 　　 家　　　↑ 　　　　　　姉が歩いた６分ぶんの距離 【弟が姉に追いついた瞬間】 　　　　　　　　　　　　　　　　○弟○ 　　　＿＿＿＿＿＿＿＿＿＿＿＿＿＿[姉] 　　 家 図はこれでＯＫ。 これは方程式の問題なので、何をＸにするかをまっ先に決めなければならない。 答えになるものをＸにするのがフツーなので、弟が家を出てから姉に追いつくまでの時間をＸ分としよう。 再度くり返すが方程式の問題なので、方程式、つまり＝でつるんだ式 をでっち上げなければならない。 ＝でつなげるもの、すなわち等しいものは何と何だろうか？ 図を見ながら考えてみよう。 すると、【弟が姉に追いついた瞬間】の図で、「姉が歩いた距離」と「弟が自転車で走った距離」の２つがドンピシャ等しいことがわかる。 これら２つを式であらわして＝でつなげば、方程式のでっち上げは完了だ。 両方とも距離なので、距離＝速さ×時間（これは知っていなけばならない）を使う。 速さは、問題に書いてある。 時間は、弟はＸ分だ。　姉は弟より６分多く歩いているから (Ｘ＋６)分になる。 よって、 姉が歩いた距離は 50(Ｘ＋６)m 弟が自転車で走った距離は 200Ｘm となるので方程式は 50(Ｘ＋６)＝200Ｘ となる。あとはこれを解くだけだ。 これで、図形以外の問題でも、図（図以外でもよい）を書くことが有効であることがおわかりいただけたと思う。 ふだんから活用されることをお祈り申しあげる。 数学の勉強,学習,受験 勉強も教える数学受験学習塾

6/15 数学・間違いだらけの暗算

今回は、「二つのタスクを暗算で同時におこなうべからず」というおはなし。 「二つのタスクを同時におこなう」 とはどういうことかというと、たとえば、「符号（＋－）を変える、というタスク」をおこないながら、同時に「式を展開する（カッコを外す）というタスク」をおこなう、ということである。 小生は数学教師のくせに暗算が不得手なので、なるべく筆算または電卓算（？）をするのであるが、小生の塾（ブログタイトルの「勉強を教えない通信教育受験塾」ではなくて、実在している学習塾）には暗算がお好きな生徒さんが多くて、上記のごとく、二つのタスクを同時に暗算でおこなっているシーンが多々見うけられる。 暗算がお好きな理由は、たぶん、時間と紙とシャーペンの芯を節約したいためであろう、と拝察申しあげている。 そして、暗算の結果、お間違えあそばす場合がひじょうに多い。 お間違えあそばすケースの筆頭二つをご紹介しよう。 【ケース１】 前記した「符号（＋－）を変えること」と「式を展開する（カッコを外す）こと」とを暗算で同時におこなってしまうケース。 実例をお見せしよう。 ［問題１］ 　a-(a+6)(b-16) を展開して簡単にせよ。 ［解答例１A］ （符号を変えるタスクと 式を展開するタスクとを暗算で同時におこなっている悪い解答例で、赤い部分がマチガイ） 　a-(a+6)(b-19) 　=a-ab+19a-6b-114 　=-ab+20a-6b-114 ［解答例１B］ （符号を変えるタスクと 式を展開するタスクとを別々に紙に書いておこなうおススメ解答例。　はじめに式の展開だけをおこない、カッコでくくっておき、つぎにそのカッコを外す、すなわち符号を変える、という方法。） 　a-(a+6)(b-19) 　=a-(ab-19a+6b-114) 　=a-ab+19a-6b+114 　=-ab+20a-6b+114 おススメ［解答例１B］は暗算［解答例１A］より１行多くなるが、ミスを犯す可能性はずっと小さくなる。 【ケース２】 分数の割り算で、「割る方の分数（÷のうしろ）を逆数にして掛け算に変換するタスク」と「掛け算計算タスク」とを同時におこなってしまうケース。 ［問題２］ 　2／3 ÷ 5／7 × 11／13 ÷ 14／15 を計算せよ。 　（少々見にくいが、「2分の1」を「1／2」と表記させていただく。） ［解答例２A］ （割る方の分数を逆数にすること と掛け算計算とを同時におこなっていて、ミスを誘発しやすい解答例で、赤い部分がNG） 　2／3 ÷ 5／7 × 11／13 ÷ 14／15 　= 14×154／15×195 　（11×15とすべきを11×14=154、13×14とすべきを13×15=195 　　と間違えている） 　= 2156／2925 ［解答例２B］ （まず逆数にすることだけを紙に書いておこない、つぎに掛け算計算（この問題では約分だけ）をおこなう、ミスをしにくいおススメ解答例） 　2／3 ÷ 5／7 × 11／13 ÷ 14／15 　= 2／3 × 7／5 × 11／13 × 15／14 　= 1／1 × 1／1 × 11／13 × 1／1　（約分の結果） 　= 11／13 この場合も前問のときと同様、おススメ解答例の方が１行多くなるが、ミスを犯す可能性が小さくなることは言うまでもない。 クルマを運転中のケータイ電話使用が法的に禁止されたことでお分かりいただけるように、人間、二つのことを同時におこなうとミスを犯しやすいのだ。 試験のときも自然におススメ解答例１B & ２B のようにやれるように、普段からタスクを分け、それを紙にお書きになることをおススメ申しあげる。 暗算解答例にくらべて１行ふえるが、頭の中でごちゃごちゃ考える必要がなくなるので、時間的にはたいして違わないのだ。 紙とシャーペンの芯は、残念ながら節約できないが、ミスを減らすための安価で有意義な投資とお考えいただければ幸いである。 数学の勉強,学習,受験 勉強も教える数学受験学習塾