7/7 数学・図形に書き込む | 勉強もたまには教える数学塾
前回(6/27 書けば解ける)の続編でありまして、
「図形に、わかっていることを(長さや角が等しい、とか平行とかを記号で)書き込むと"御利益"がある」
というおはなし。
前回と同様、問題を例にして説明させていただく。
【 問題 】
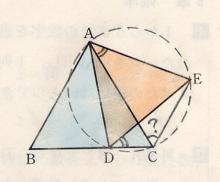
図のように、頂点Aが重なる正三角形ABCと正三角形ADEがある。
Dが辺BC上にあるとき、∠ACEの大きさを求めよ。
(中学2年の数学教科書に載っている問題である。)
まず、記号が書き込まれていない下図を見て、お考えいただきたい。

なかなか妙案が浮かばないのではないだろうか?
(スラスラ出来ちまった方は前回同様、以下の駄文はお読みになる必要はない。
ゲームのつづきでもやってください。)
では、長さについて等しいことを示す記号を書き込んだ次の図をご覧いただきたい。

すると、求めるべき∠ACE(?マークの角)を含む△ACEと、それと形が似ている△ABDの二つについて、等しいという記号がついている辺は、
AC=AB・・・① と
AE=AD・・・②
であることが容易にわかる。
ここで、もし
∠CAE=∠BAD・・・③
であれば、①,②といっしょになって、三角形の合同条件のひとつである
「2辺とその間の角がそれぞれ等しい」
がOKになるので、両三角形は合同になり、したがって
∠ACE=∠B=60°
となって、一件落着と相成る。
(∠B=60°の理由:△ABCは正三角形なので3つの角はすべて60°)
そこで、③がOKかどうかだが、③の両辺は、正三角形の1つの角(∠DAE、∠BAC)すなわち60°からそれぞれ同じ∠DACを差し引いたものであって、式に書けば、
∠CAE=∠DAE-∠DAC=60°-∠DAC
∠BAD=∠BAC-∠DAC=60°-∠DAC
よって
∠CAE=∠BAD (③と同じ)
であるから、③は100%OKである。
したがって、正解は
∠ACE=60° でゴザル。
さて、はなしを本題にもどして、この問題が解けるか否かは、「△ACEと△ABDが合同であること」に気がつくことに懸かっており、上の2つの図のどちらが気づき易いかといえば、モチ、下の記号入りの図の方であろう。
「上の図の方」とお答えの方には、お臍がまっすぐかどうかご点検をおすすめする。
以上のことから、図に記号を書き込むと御利益があることをご理解いただけたと思う。
おおいに利用していただきたい。
なお、下記のようなビューティフルな別解もあるので、ご参考まで。
ただし、現行(H13年検定)の教科書の記述を少し超えるが。
(旧教科書ではセーフである。)
【別解】
△ADEは、はじめ、AD,AEがそれぞれAB,ACに重なる位置にあったとし、その位置から点Aを中心として反時計回りの向きに∠CAEだけ回転移動したと考える。
また、はじめの位置では DE//BC すなわち DEとBCのなす角は0°であったから
∠CAE=∠CDE (両方とも回転した角)
さらに、点D,C,Eを通る円において、点Aは弦CEについて弧CDEと同じ側にある。
この2つのことから、定理(*)により、点Aは弧CDE上にあることになる。
すなわち4点A,D,C,E は同一円周上にある。
そして、∠ACEと∠ADEは共通の弧AEに対する円周角になっている。
したがって定理(**)により
∠ACE=∠ADE=60°
(別解END)
定理(*)
円Oで、点Qが弦ABについて弧APBと同じ側にあって、
∠AQB=∠APBならば、点Qは弧APB上にある。
(現行教科書では削除されている。)
定理(**)
同じ弧に対する円周角の大きさはすべて等しい。
この別解をビューティフルと思っていただけるか否かは、もちろん貴下のご自由である。
数学の勉強,学習,受験
勉強も教える数学受験学習塾
|

